Advancing statistical methods for X-ray spectra

Kaffeerunde / Apr 2014

Johannes Buchner / MPE

in collaboration with A. Georgakakis, K. Nandra, L. Hsu, C. Rangel, M. Brightman, A. Merloni and M. Salvato

Buchner et al. 2014 - arxiv:1402.0004
X-ray spectral modelling of the AGN obscuring region in the CDFS: Bayesian model selection and catalogue

github.com/JohannesBuchner/BXA

Introduction

X-ray data + background data
Set/fit background model
Define source model 3-20 parameters
Set Poisson likelihood (C-Stat), no re-binning
How to attack this parameter space?

Model comparison

Likelihood ratio tests / F-test

only if special case
not at borders (feature detection)
only if $n\rightarrow\infty$
do not compute it, interpretation is wrong; critisize papers mis-interpreting the statistic

Pragmatic viewpoint

distinguish two models via data can use any statistic

does not have to be probabilistic

can be counts in the 6keV bin
determine discriminating threshold via simulations
- false association rate ($B\rightarrow A$, $A\rightarrow B$)
- correct association rate ($A\rightarrow A$, $B\rightarrow B$)

Comparison $\hat{L}$ vs. $Z$

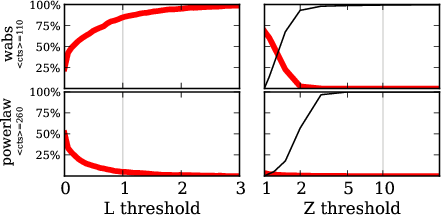red: falsely choose powerlaw, for wabs input

red: falsely choose wabs, for powerlaw input

(Appendix 2)

$Z$ more effective than $\hat{L}$

what is $Z$? Integral of likelihood / average

Bayesian evidence $$ {P(A|D)\over P(B|D)} = {P(A)\over P(B)} \times {Z_A\over Z_B} $$

interpretation of Z-ratio under flat priors:

prob. that this model is the right one, rather than the other.
A, B or equal

How to compute integral?

More motivation

Best fit alone does not mean anything. Need uncertainties.

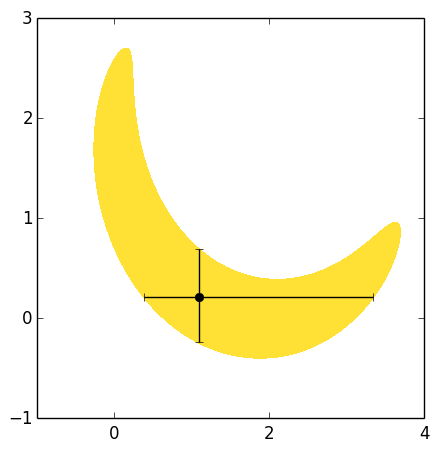1d search: underestimates uncertainties
2d contours: solve (computationally expensively) in 2d What about the other 10d?
Fisher matrix/Hessian: only for simple correlations, not bananas

Example: Absorbed powerlaw on background

two solutions

(Appendix 3)

Example: Absorbed powerlaw on background

Occurs in real data
We just do not know which solution is the right one (uncertain)
keep both!
measure both/all!
not just in 2d, but n-dim; not user-specified

Nested Sampling

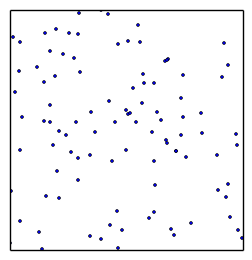draw randomly uniformly 200 points
always remove least likely point, replace with a new draw of higher likelihood

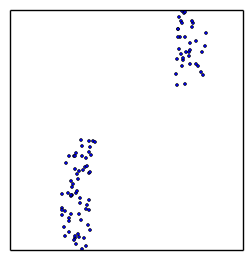converges to maximum likelihood, stops when flat

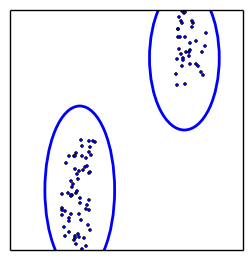how to draw new points efficiently?
MultiNest does it via clustering and ellipses

Nested Sampling with MultiNest

explores the problem in

high dimensions (3-20)
handles multiple maxima
handles peculiar shapes
runs efficiently to convergence
(typically 10000-40000 points)

measures and describes shapes (like MCMC)

Connecting

Need to connect C-stat calculation with algorithm

BXA: Bayesian X-ray Analysis

MultiNest for Sherpa / (Py)Xspec
installed on ds42 under
```
/utils/bxa
```
documentation: github.com/JohannesBuchner/BXA

Analysis

Likelihood value evaluated "everywhere"

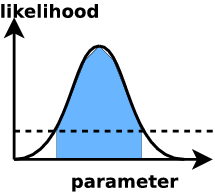ML analysis: find confidence intervals
- defined via: how often the estimator (maximum) gives the right answer
- different for different estimators - property of the method
credible intervals
- defined via: prob. that the true value is inside this range rather than outside is x%.

results coincide for some choice of prior (usually "flat").

How?

posterior "chain" from MCMC/nested sampling: representation through point density

norm	$N_H$	$z$
-4.1	22.4	2.3
-4.3	22.45	2.4
-4.3	22.38	2.5
...	...

just make histogram of 1/2 columns

contains all correlations

Error propagation: example

norm	$N_H$	$z$
-4.1	22.4	2.3
-4.3	22.45	2.4
-4.3	22.38	2.5
...	...

for every parameter vector
(norm, $N_H$, $z$, ...), set the model

set $N_H$ = 0
compute intrinsic flux
compute luminosity
using $z$ and flux

incorporates uncertainty in $z$ and the parameters!

just do your calculation with every value instead of one

model inadequacy

Have cool tools now, but:

Is the model right?
Where is the model wrong?
Systematic effects?
Discover new physics beyond the model

Common route: residuals

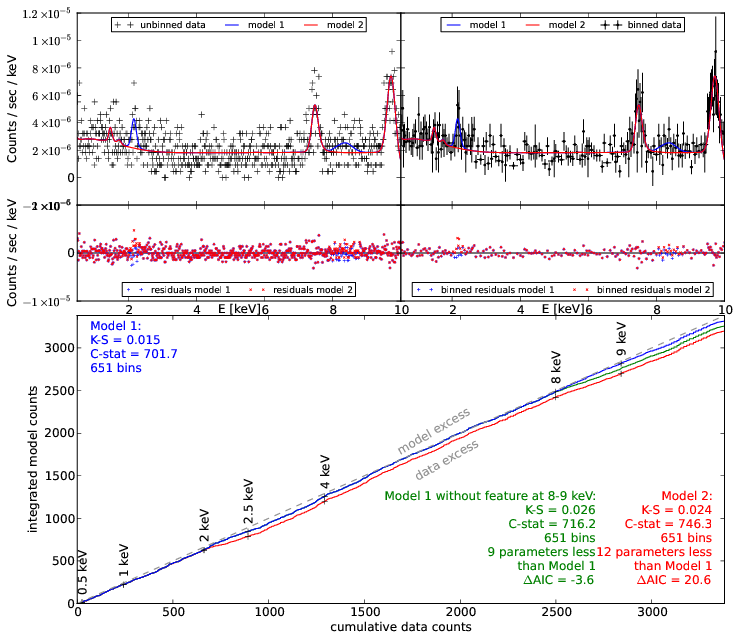
New idea: Q-Q plot (no binning)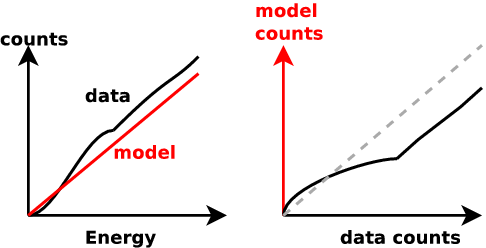

(Appendix 1)

good fit if straight line

Q-Q plot primer

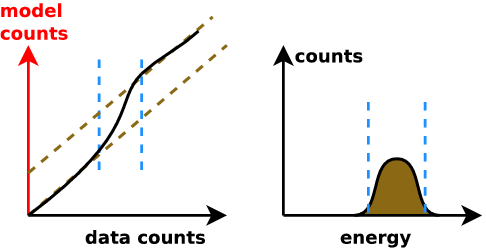
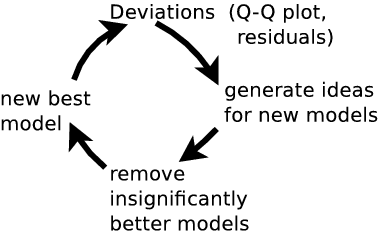
Generate ideas for new models

Summary

(see 5.1, Appendix 3)
Parameter estimation:
explore multiple maxima
general solution with nested sampling
Model comparison:
Likelihood ratio is less effective than Z ratios
(see 5.2, Appendix 2)

computed by nested sampling; has right interpretation
(see 5.3, Appendix 1)
Model discovery:
Q-Q plots + model comparison

arxiv:1402.0004 github.com/JohannesBuchner/BXA