line - cylinder intersection -- Intersection formulas for 3d objects

line - cylinder intersection

Equation for line (cartesian)

x: $t + x_{0}$
y: $k t + y_{0}$
z: $l t + z_{0}$

Equation for cylinder (cartesian)

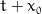
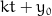
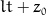
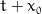
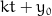
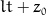
Assumed to be centred at 0, the coordinate system origin.

0=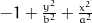 $-1 + \frac{y^{2}}{b^{2}} + \frac{x^{2}}{a^{2}}$

Intersection solutions

Parametric solution (t). Solutions were derived automatically using sympy.

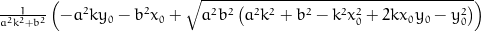
$\frac{1}{a^{2} k^{2} + b^{2}} \left(- a^{2} k y_{0} - b^{2} x_{0} + \sqrt{a^{2} b^{2} \left(a^{2} k^{2} + b^{2} - k^{2} x_{0}^{2} + 2 k x_{0} y_{0} - y_{0}^{2}\right)}\right)$
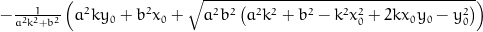
$- \frac{1}{a^{2} k^{2} + b^{2}} \left(a^{2} k y_{0} + b^{2} x_{0} + \sqrt{a^{2} b^{2} \left(a^{2} k^{2} + b^{2} - k^{2} x_{0}^{2} + 2 k x_{0} y_{0} - y_{0}^{2}\right)}\right)$

Points in cartesian coordinates (x, y, z)

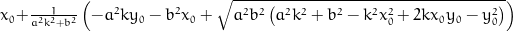
- x: $x_{0} + \frac{1}{a^{2} k^{2} + b^{2}} \left(- a^{2} k y_{0} - b^{2} x_{0} + \sqrt{a^{2} b^{2} \left(a^{2} k^{2} + b^{2} - k^{2} x_{0}^{2} + 2 k x_{0} y_{0} - y_{0}^{2}\right)}\right)$
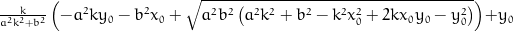
- y: $\frac{k}{a^{2} k^{2} + b^{2}} \left(- a^{2} k y_{0} - b^{2} x_{0} + \sqrt{a^{2} b^{2} \left(a^{2} k^{2} + b^{2} - k^{2} x_{0}^{2} + 2 k x_{0} y_{0} - y_{0}^{2}\right)}\right) + y_{0}$
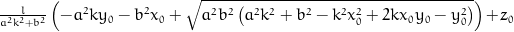
- z: $\frac{l}{a^{2} k^{2} + b^{2}} \left(- a^{2} k y_{0} - b^{2} x_{0} + \sqrt{a^{2} b^{2} \left(a^{2} k^{2} + b^{2} - k^{2} x_{0}^{2} + 2 k x_{0} y_{0} - y_{0}^{2}\right)}\right) + z_{0}$
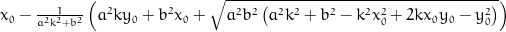
- x: $x_{0} - \frac{1}{a^{2} k^{2} + b^{2}} \left(a^{2} k y_{0} + b^{2} x_{0} + \sqrt{a^{2} b^{2} \left(a^{2} k^{2} + b^{2} - k^{2} x_{0}^{2} + 2 k x_{0} y_{0} - y_{0}^{2}\right)}\right)$
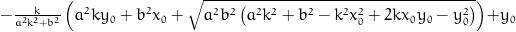
- y: $- \frac{k}{a^{2} k^{2} + b^{2}} \left(a^{2} k y_{0} + b^{2} x_{0} + \sqrt{a^{2} b^{2} \left(a^{2} k^{2} + b^{2} - k^{2} x_{0}^{2} + 2 k x_{0} y_{0} - y_{0}^{2}\right)}\right) + y_{0}$
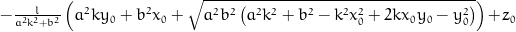
- z: $- \frac{l}{a^{2} k^{2} + b^{2}} \left(a^{2} k y_{0} + b^{2} x_{0} + \sqrt{a^{2} b^{2} \left(a^{2} k^{2} + b^{2} - k^{2} x_{0}^{2} + 2 k x_{0} y_{0} - y_{0}^{2}\right)}\right) + z_{0}$

C Code

x = x0 + (-pow(a, 2)*k*y0 - pow(b, 2)*x0 + sqrt(pow(a, 2)*pow(b, 2)*(pow(a, 2)*pow(k, 2) + pow(b, 2) - pow(k, 2)*pow(x0, 2) + 2*k*x0*y0 - pow(y0, 2))))/(pow(a, 2)*pow(k, 2) + pow(b, 2));

y = k*(-pow(a, 2)*k*y0 - pow(b, 2)*x0 + sqrt(pow(a, 2)*pow(b, 2)*(pow(a, 2)*pow(k, 2) + pow(b, 2) - pow(k, 2)*pow(x0, 2) + 2*k*x0*y0 - pow(y0, 2))))/(pow(a, 2)*pow(k, 2) + pow(b, 2)) + y0;

z = l*(-pow(a, 2)*k*y0 - pow(b, 2)*x0 + sqrt(pow(a, 2)*pow(b, 2)*(pow(a, 2)*pow(k, 2) + pow(b, 2) - pow(k, 2)*pow(x0, 2) + 2*k*x0*y0 - pow(y0, 2))))/(pow(a, 2)*pow(k, 2) + pow(b, 2)) + z0;

x = x0 - (pow(a, 2)*k*y0 + pow(b, 2)*x0 + sqrt(pow(a, 2)*pow(b, 2)*(pow(a, 2)*pow(k, 2) + pow(b, 2) - pow(k, 2)*pow(x0, 2) + 2*k*x0*y0 - pow(y0, 2))))/(pow(a, 2)*pow(k, 2) + pow(b, 2));

y = -k*(pow(a, 2)*k*y0 + pow(b, 2)*x0 + sqrt(pow(a, 2)*pow(b, 2)*(pow(a, 2)*pow(k, 2) + pow(b, 2) - pow(k, 2)*pow(x0, 2) + 2*k*x0*y0 - pow(y0, 2))))/(pow(a, 2)*pow(k, 2) + pow(b, 2)) + y0;

z = -l*(pow(a, 2)*k*y0 + pow(b, 2)*x0 + sqrt(pow(a, 2)*pow(b, 2)*(pow(a, 2)*pow(k, 2) + pow(b, 2) - pow(k, 2)*pow(x0, 2) + 2*k*x0*y0 - pow(y0, 2))))/(pow(a, 2)*pow(k, 2) + pow(b, 2)) + z0;

Distance inside

Distance between crossing points.

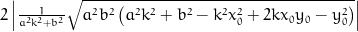
$2 \left\lvert{\frac{1}{a^{2} k^{2} + b^{2}} \sqrt{a^{2} b^{2} \left(a^{2} k^{2} + b^{2} - k^{2} x_{0}^{2} + 2 k x_{0} y_{0} - y_{0}^{2}\right)}}\right\rvert$

C Code

sol1 = (-pow(a, 2)*k*y0 - pow(b, 2)*x0 + sqrt(pow(a, 2)*pow(b, 2)*(pow(a, 2)*pow(k, 2) + pow(b, 2) - pow(k, 2)*pow(x0, 2) + 2*k*x0*y0 - pow(y0, 2))))/(pow(a, 2)*pow(k, 2) + pow(b, 2));

sol2 = -(pow(a, 2)*k*y0 + pow(b, 2)*x0 + sqrt(pow(a, 2)*pow(b, 2)*(pow(a, 2)*pow(k, 2) + pow(b, 2) - pow(k, 2)*pow(x0, 2) + 2*k*x0*y0 - pow(y0, 2))))/(pow(a, 2)*pow(k, 2) + pow(b, 2));

distance = 2*fabs(sqrt(pow(a, 2)*pow(b, 2)*(pow(a, 2)*pow(k, 2) + pow(b, 2) - pow(k, 2)*pow(x0, 2) + 2*k*x0*y0 - pow(y0, 2)))/(pow(a, 2)*pow(k, 2) + pow(b, 2)));

Equation for line (spherical)

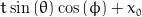
x: $t \sin{\left (\theta \right )} \cos{\left (\phi \right )} + x_{0}$
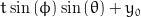
y: $t \sin{\left (\phi \right )} \sin{\left (\theta \right )} + y_{0}$
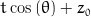
z: $t \cos{\left (\theta \right )} + z_{0}$

Equation for cylinder (cartesian)

Assumed to be centred at 0, the coordinate system origin.

0=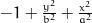 $-1 + \frac{y^{2}}{b^{2}} + \frac{x^{2}}{a^{2}}$

Intersection solutions

Parametric solution (t). Solutions were derived automatically using sympy.

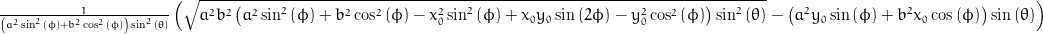
$\frac{1}{\left(a^{2} \sin^{2}{\left (\phi \right )} + b^{2} \cos^{2}{\left (\phi \right )}\right) \sin^{2}{\left (\theta \right )}} \left(\sqrt{a^{2} b^{2} \left(a^{2} \sin^{2}{\left (\phi \right )} + b^{2} \cos^{2}{\left (\phi \right )} - x_{0}^{2} \sin^{2}{\left (\phi \right )} + x_{0} y_{0} \sin{\left (2 \phi \right )} - y_{0}^{2} \cos^{2}{\left (\phi \right )}\right) \sin^{2}{\left (\theta \right )}} - \left(a^{2} y_{0} \sin{\left (\phi \right )} + b^{2} x_{0} \cos{\left (\phi \right )}\right) \sin{\left (\theta \right )}\right)$
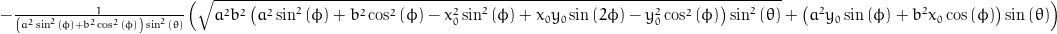
$- \frac{1}{\left(a^{2} \sin^{2}{\left (\phi \right )} + b^{2} \cos^{2}{\left (\phi \right )}\right) \sin^{2}{\left (\theta \right )}} \left(\sqrt{a^{2} b^{2} \left(a^{2} \sin^{2}{\left (\phi \right )} + b^{2} \cos^{2}{\left (\phi \right )} - x_{0}^{2} \sin^{2}{\left (\phi \right )} + x_{0} y_{0} \sin{\left (2 \phi \right )} - y_{0}^{2} \cos^{2}{\left (\phi \right )}\right) \sin^{2}{\left (\theta \right )}} + \left(a^{2} y_{0} \sin{\left (\phi \right )} + b^{2} x_{0} \cos{\left (\phi \right )}\right) \sin{\left (\theta \right )}\right)$

Points in cartesian coordinates (x, y, z)

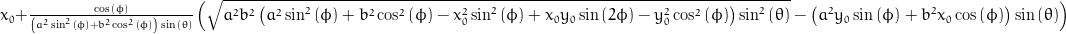
- x: $x_{0} + \frac{\cos{\left (\phi \right )}}{\left(a^{2} \sin^{2}{\left (\phi \right )} + b^{2} \cos^{2}{\left (\phi \right )}\right) \sin{\left (\theta \right )}} \left(\sqrt{a^{2} b^{2} \left(a^{2} \sin^{2}{\left (\phi \right )} + b^{2} \cos^{2}{\left (\phi \right )} - x_{0}^{2} \sin^{2}{\left (\phi \right )} + x_{0} y_{0} \sin{\left (2 \phi \right )} - y_{0}^{2} \cos^{2}{\left (\phi \right )}\right) \sin^{2}{\left (\theta \right )}} - \left(a^{2} y_{0} \sin{\left (\phi \right )} + b^{2} x_{0} \cos{\left (\phi \right )}\right) \sin{\left (\theta \right )}\right)$
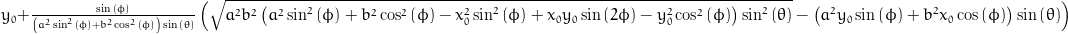
- y: $y_{0} + \frac{\sin{\left (\phi \right )}}{\left(a^{2} \sin^{2}{\left (\phi \right )} + b^{2} \cos^{2}{\left (\phi \right )}\right) \sin{\left (\theta \right )}} \left(\sqrt{a^{2} b^{2} \left(a^{2} \sin^{2}{\left (\phi \right )} + b^{2} \cos^{2}{\left (\phi \right )} - x_{0}^{2} \sin^{2}{\left (\phi \right )} + x_{0} y_{0} \sin{\left (2 \phi \right )} - y_{0}^{2} \cos^{2}{\left (\phi \right )}\right) \sin^{2}{\left (\theta \right )}} - \left(a^{2} y_{0} \sin{\left (\phi \right )} + b^{2} x_{0} \cos{\left (\phi \right )}\right) \sin{\left (\theta \right )}\right)$
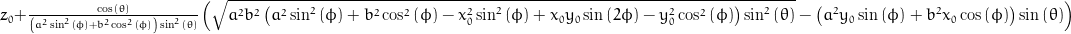
- z: $z_{0} + \frac{\cos{\left (\theta \right )}}{\left(a^{2} \sin^{2}{\left (\phi \right )} + b^{2} \cos^{2}{\left (\phi \right )}\right) \sin^{2}{\left (\theta \right )}} \left(\sqrt{a^{2} b^{2} \left(a^{2} \sin^{2}{\left (\phi \right )} + b^{2} \cos^{2}{\left (\phi \right )} - x_{0}^{2} \sin^{2}{\left (\phi \right )} + x_{0} y_{0} \sin{\left (2 \phi \right )} - y_{0}^{2} \cos^{2}{\left (\phi \right )}\right) \sin^{2}{\left (\theta \right )}} - \left(a^{2} y_{0} \sin{\left (\phi \right )} + b^{2} x_{0} \cos{\left (\phi \right )}\right) \sin{\left (\theta \right )}\right)$
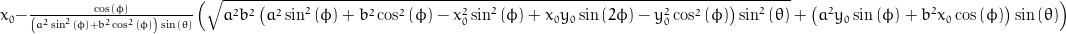
- x: $x_{0} - \frac{\cos{\left (\phi \right )}}{\left(a^{2} \sin^{2}{\left (\phi \right )} + b^{2} \cos^{2}{\left (\phi \right )}\right) \sin{\left (\theta \right )}} \left(\sqrt{a^{2} b^{2} \left(a^{2} \sin^{2}{\left (\phi \right )} + b^{2} \cos^{2}{\left (\phi \right )} - x_{0}^{2} \sin^{2}{\left (\phi \right )} + x_{0} y_{0} \sin{\left (2 \phi \right )} - y_{0}^{2} \cos^{2}{\left (\phi \right )}\right) \sin^{2}{\left (\theta \right )}} + \left(a^{2} y_{0} \sin{\left (\phi \right )} + b^{2} x_{0} \cos{\left (\phi \right )}\right) \sin{\left (\theta \right )}\right)$
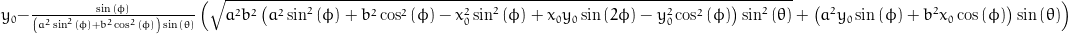
- y: $y_{0} - \frac{\sin{\left (\phi \right )}}{\left(a^{2} \sin^{2}{\left (\phi \right )} + b^{2} \cos^{2}{\left (\phi \right )}\right) \sin{\left (\theta \right )}} \left(\sqrt{a^{2} b^{2} \left(a^{2} \sin^{2}{\left (\phi \right )} + b^{2} \cos^{2}{\left (\phi \right )} - x_{0}^{2} \sin^{2}{\left (\phi \right )} + x_{0} y_{0} \sin{\left (2 \phi \right )} - y_{0}^{2} \cos^{2}{\left (\phi \right )}\right) \sin^{2}{\left (\theta \right )}} + \left(a^{2} y_{0} \sin{\left (\phi \right )} + b^{2} x_{0} \cos{\left (\phi \right )}\right) \sin{\left (\theta \right )}\right)$
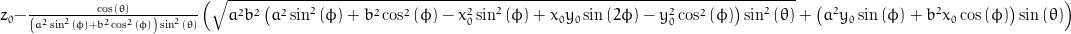
- z: $z_{0} - \frac{\cos{\left (\theta \right )}}{\left(a^{2} \sin^{2}{\left (\phi \right )} + b^{2} \cos^{2}{\left (\phi \right )}\right) \sin^{2}{\left (\theta \right )}} \left(\sqrt{a^{2} b^{2} \left(a^{2} \sin^{2}{\left (\phi \right )} + b^{2} \cos^{2}{\left (\phi \right )} - x_{0}^{2} \sin^{2}{\left (\phi \right )} + x_{0} y_{0} \sin{\left (2 \phi \right )} - y_{0}^{2} \cos^{2}{\left (\phi \right )}\right) \sin^{2}{\left (\theta \right )}} + \left(a^{2} y_{0} \sin{\left (\phi \right )} + b^{2} x_{0} \cos{\left (\phi \right )}\right) \sin{\left (\theta \right )}\right)$

C Code

x = x0 + (sqrt(pow(a, 2)*pow(b, 2)*(pow(a, 2)*pow(sin(phi), 2) + pow(b, 2)*pow(cos(phi), 2) - pow(x0, 2)*pow(sin(phi), 2) + x0*y0*sin(2*phi) - pow(y0, 2)*pow(cos(phi), 2))*pow(sin(theta), 2)) - (pow(a, 2)*y0*sin(phi) + pow(b, 2)*x0*cos(phi))*sin(theta))*cos(phi)/((pow(a, 2)*pow(sin(phi), 2) + pow(b, 2)*pow(cos(phi), 2))*sin(theta));

y = y0 + (sqrt(pow(a, 2)*pow(b, 2)*(pow(a, 2)*pow(sin(phi), 2) + pow(b, 2)*pow(cos(phi), 2) - pow(x0, 2)*pow(sin(phi), 2) + x0*y0*sin(2*phi) - pow(y0, 2)*pow(cos(phi), 2))*pow(sin(theta), 2)) - (pow(a, 2)*y0*sin(phi) + pow(b, 2)*x0*cos(phi))*sin(theta))*sin(phi)/((pow(a, 2)*pow(sin(phi), 2) + pow(b, 2)*pow(cos(phi), 2))*sin(theta));

z = z0 + (sqrt(pow(a, 2)*pow(b, 2)*(pow(a, 2)*pow(sin(phi), 2) + pow(b, 2)*pow(cos(phi), 2) - pow(x0, 2)*pow(sin(phi), 2) + x0*y0*sin(2*phi) - pow(y0, 2)*pow(cos(phi), 2))*pow(sin(theta), 2)) - (pow(a, 2)*y0*sin(phi) + pow(b, 2)*x0*cos(phi))*sin(theta))*cos(theta)/((pow(a, 2)*pow(sin(phi), 2) + pow(b, 2)*pow(cos(phi), 2))*pow(sin(theta), 2));

x = x0 - (sqrt(pow(a, 2)*pow(b, 2)*(pow(a, 2)*pow(sin(phi), 2) + pow(b, 2)*pow(cos(phi), 2) - pow(x0, 2)*pow(sin(phi), 2) + x0*y0*sin(2*phi) - pow(y0, 2)*pow(cos(phi), 2))*pow(sin(theta), 2)) + (pow(a, 2)*y0*sin(phi) + pow(b, 2)*x0*cos(phi))*sin(theta))*cos(phi)/((pow(a, 2)*pow(sin(phi), 2) + pow(b, 2)*pow(cos(phi), 2))*sin(theta));

y = y0 - (sqrt(pow(a, 2)*pow(b, 2)*(pow(a, 2)*pow(sin(phi), 2) + pow(b, 2)*pow(cos(phi), 2) - pow(x0, 2)*pow(sin(phi), 2) + x0*y0*sin(2*phi) - pow(y0, 2)*pow(cos(phi), 2))*pow(sin(theta), 2)) + (pow(a, 2)*y0*sin(phi) + pow(b, 2)*x0*cos(phi))*sin(theta))*sin(phi)/((pow(a, 2)*pow(sin(phi), 2) + pow(b, 2)*pow(cos(phi), 2))*sin(theta));

z = z0 - (sqrt(pow(a, 2)*pow(b, 2)*(pow(a, 2)*pow(sin(phi), 2) + pow(b, 2)*pow(cos(phi), 2) - pow(x0, 2)*pow(sin(phi), 2) + x0*y0*sin(2*phi) - pow(y0, 2)*pow(cos(phi), 2))*pow(sin(theta), 2)) + (pow(a, 2)*y0*sin(phi) + pow(b, 2)*x0*cos(phi))*sin(theta))*cos(theta)/((pow(a, 2)*pow(sin(phi), 2) + pow(b, 2)*pow(cos(phi), 2))*pow(sin(theta), 2));

Distance inside

Distance between crossing points.

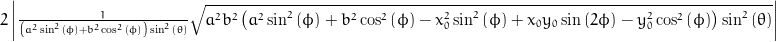
$2 \left\lvert{\frac{1}{\left(a^{2} \sin^{2}{\left (\phi \right )} + b^{2} \cos^{2}{\left (\phi \right )}\right) \sin^{2}{\left (\theta \right )}} \sqrt{a^{2} b^{2} \left(a^{2} \sin^{2}{\left (\phi \right )} + b^{2} \cos^{2}{\left (\phi \right )} - x_{0}^{2} \sin^{2}{\left (\phi \right )} + x_{0} y_{0} \sin{\left (2 \phi \right )} - y_{0}^{2} \cos^{2}{\left (\phi \right )}\right) \sin^{2}{\left (\theta \right )}}}\right\rvert$

C Code

sol1 = (sqrt(pow(a, 2)*pow(b, 2)*(pow(a, 2)*pow(sin(phi), 2) + pow(b, 2)*pow(cos(phi), 2) - pow(x0, 2)*pow(sin(phi), 2) + x0*y0*sin(2*phi) - pow(y0, 2)*pow(cos(phi), 2))*pow(sin(theta), 2)) - (pow(a, 2)*y0*sin(phi) + pow(b, 2)*x0*cos(phi))*sin(theta))/((pow(a, 2)*pow(sin(phi), 2) + pow(b, 2)*pow(cos(phi), 2))*pow(sin(theta), 2));

sol2 = -(sqrt(pow(a, 2)*pow(b, 2)*(pow(a, 2)*pow(sin(phi), 2) + pow(b, 2)*pow(cos(phi), 2) - pow(x0, 2)*pow(sin(phi), 2) + x0*y0*sin(2*phi) - pow(y0, 2)*pow(cos(phi), 2))*pow(sin(theta), 2)) + (pow(a, 2)*y0*sin(phi) + pow(b, 2)*x0*cos(phi))*sin(theta))/((pow(a, 2)*pow(sin(phi), 2) + pow(b, 2)*pow(cos(phi), 2))*pow(sin(theta), 2));

distance = 2*fabs(sqrt(pow(a, 2)*pow(b, 2)*(pow(a, 2)*pow(sin(phi), 2) + pow(b, 2)*pow(cos(phi), 2) - pow(x0, 2)*pow(sin(phi), 2) + x0*y0*sin(2*phi) - pow(y0, 2)*pow(cos(phi), 2))*pow(sin(theta), 2))/((pow(a, 2)*pow(sin(phi), 2) + pow(b, 2)*pow(cos(phi), 2))*pow(sin(theta), 2)));

By Johannes Buchner | Source code: https://github.com/JohannesBuchner/intersection | Open a issue or pull request if you would like somthing added