PyMultiNest tutorial

Casual parameter estimation and model selection

Johannes Buchner

Max Planck Institute for Extraterrestrial Physics

November 2013

About me

implemented MCMC sampler for Bachelor thesis
since then, 5 years of experience with Monte Carlo methods for Bayesian inference
Numerical Likelihood functions (0.1-5s), low-dimensional (<20)
Research on accreting supermassive black hole in X-ray (Poisson spectra)
Recent interest: smooth field reconstruction with numerical likelihoods (20-500 dimensions)

https://www.mpe.mpg.de/~jbuchner/ -- Johannes Buchner

Go-to Methods

(for numerical likelihoods)

Parameter estimation

Optimize to maximum (ML/MAP)
explore around it with MCMC
High-dimensional, misbehaved: MCMC (?), HMC (?)

Model selection

High-dimensional:
Low-dimensional:
Nested models:

Tools so far

(for numerical likelihoods)

Parameter estimation

Optimize to maximum (ML/MAP)
explore around it with MCMC
High-dimensional, misbehaved: MCMC (?), HMC (?)
Low-dimensional, multi-modal: MultiNest

Model selection

High-dimensional: give up
Low-dimensional (<20), multi-modal: MultiNest
Nested models: AIC + DE

also for Low-dimensional, multi-modal: MultiNest

What will we do today?

Goal: solving $Z$ integrals

Write likelihood functions
Write prior functions
run nested sampling code
look at marginal plots and compare evidence $Z$

Software: PyMultiNest

based on MultiNest: written by Farhan Feroz and Mike Hobson (2007)
Finds clusters -> sampling from ellipses
Python instead of writing Fortran or C functions
parses output, and does a bit of plotting
Also produces "Markov Chain" for uncertainty propagation

Prior functions: A math trick

Based on transforming unit cube:

$\int_a^b{f(x)g(x) dx} = \int_0^1{f(G^{-1}(u))~ du}$

where $G$ is the cumulative distribution of $g$ :

$G(x) = \int_{-\infty}^{x}{g(x') dx'}, G(a) = 0, G(b) = 1$

transformation through inverse of CDF
compresses unimportant regions
"native units": $P(\theta|D)\propto \int_0^1{P(D|u) du}$
can also do this in MCMC!

Prior functions: A math trick

Transform from unit cube to parameter space
Using inverse CDF of prior


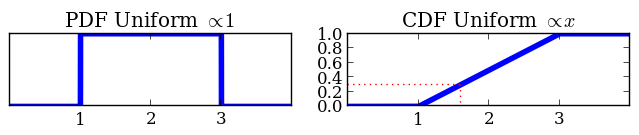
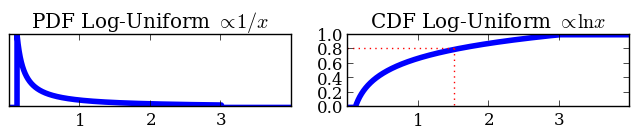
def prior(cube, ndim, nparams):
	cube[0] = cube[0] * (3 - 1) + 1
	cube[1] = 10**(cube[1] * (1 + 0.5) - 1)

Shortest Code Example

import pymultinest

def prior(cube, ndim, nparams):
	cube[0] = cube[0] * 2

def loglikelihood(cube, ndim, nparams):
	return -0.5 * ((cube[0] - 0.2) / 0.1)**2

pymultinest.run(loglikelihood, prior, n_params=1)

Prior ~ $U(0, 2)$
Likelihood ~ $N(\mu=0.2, \sigma=0.1)$
1d

Tutorial

http://johannesbuchner.github.io/pymultinest-tutorial/

$ ssh -Y schoolNN@naf-school01.desy.de
$ bash
$ source /afs/desy.de/group/school/mc-school/setup_pymultinest.sh
$ git clone https://github.com/JohannesBuchner/pymultinest-tutorial

Example 1: 1d multi-modal problem
Example 2: Spectral line analysis -- 1 line or 2 lines?
Example 3: Hierarchical Bayes, Your own, Lighthouse problem, further reading

Final points

Correlation of parameters from posterior samples SysCorr
Throw multiple algorithms against problem (jbopt)
Fully automated model selection, but is model a good one? Systematic errors? Confidence on model choice?
PyMultiNest reference: Buchner et al (in prep), MultiNest: arXiv:0704.3704, arXiv:0809.3437 & arXiv:1306.2144